桜蔭算数の過去問
問題(桜蔭中2007)

図1は表面が同じ大きさの正三角形4個からなる立体で正四面体といいます。
図2は表面が同じ大きさの正方形6個からなる立体で立方体といいます。
図3は表面が同じ大きさの正三角形8個からなる立体で正八面体といいます。
図4は表面が同じ大きさの正五角形12個からなる立体で正十二面体といいます。
図5は表面が同じ大きさの正三角形20個からなる立体で正二十面体といいます。
これらの立体の辺をカッターで切り,開いて平面にすることを考えます。そのとき,辺以外は切らないものとし,切り開いてできたものは2枚以上に分かれていないようにします。いくつの辺を切ればよいかを考えます。
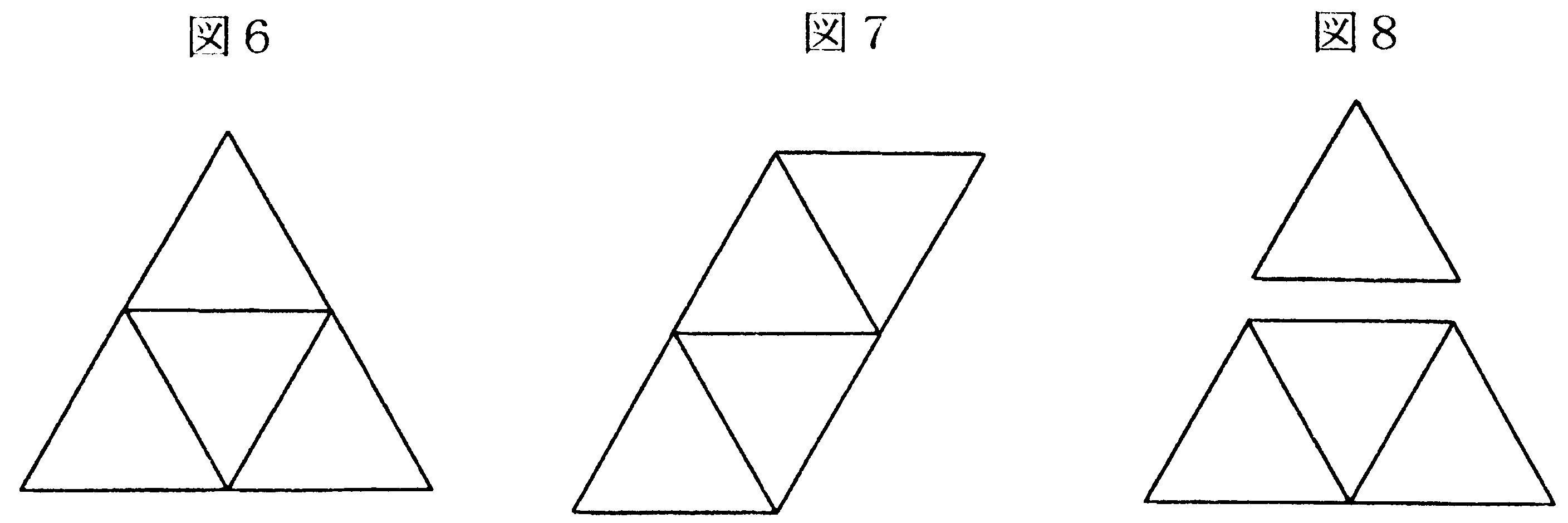
(例)図1の場合,3つの辺を切ると図6または図7のようになります。図8のように4つの辺を切ると2枚に分かれるので条件にあいません。よって切る辺の数は3です。
図2,図3,図4,図5の場合はそれぞれいくつの辺を切ればよいですか。辺の数を答えなさい。