市川の過去問
算数の問題(市川中2018)
下の図の三角形ABCは,AB=ACの二等辺三角形です。三角形ABCの内部にAP=PQ=QR=…=BCとなる二等辺三角形をつくると,三角形ABCの内部にすき間なく22個の二等辺三角形ができました。頂点Aに近い二等辺三角形から順に,1,2,3,・‥,22と番号をつけます。このとき,次の問いに答えなさい。
(1) 角ABCの大きさを求めなさい。
(2) 1から22までの二等辺三角形の中で,面積が最も大きいのは,何番の二等辺三角形ですか。

算数の問題(市川中2018)
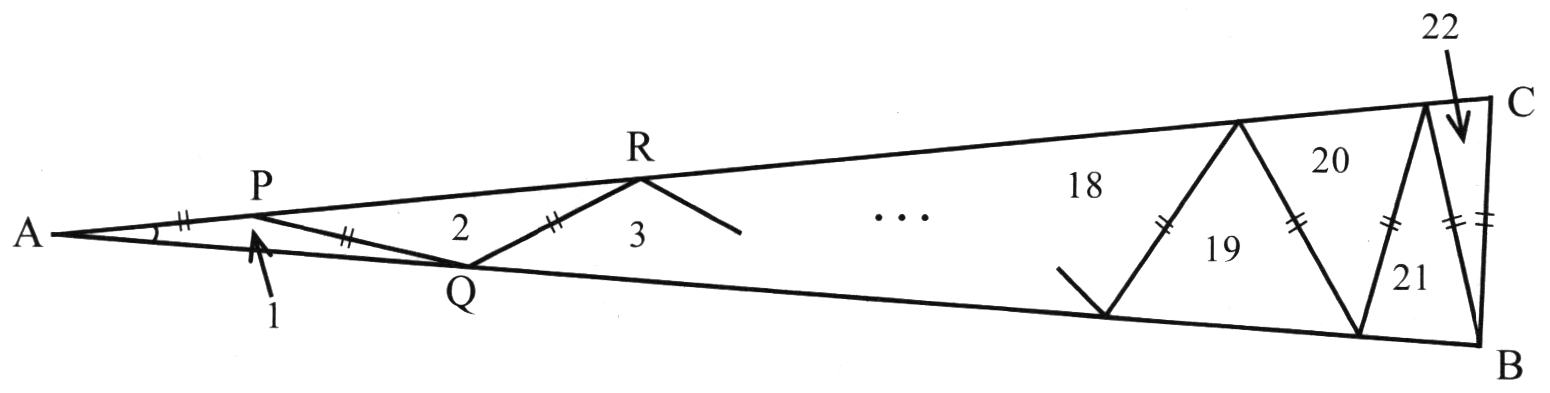
下の図の三角形ABCは,AB=ACの二等辺三角形です。三角形ABCの内部にAP=PQ=QR=…=BCとなる二等辺三角形をつくると,三角形ABCの内部にすき間なく22個の二等辺三角形ができました。頂点Aに近い二等辺三角形から順に,1,2,3,・‥,22と番号をつけます。このとき,次の問いに答えなさい。
(1) 角ABCの大きさを求めなさい。
(2) 1から22までの二等辺三角形の中で,面積が最も大きいのは,何番の二等辺三角形ですか。

© 2018 G Labo, Genius