算数の問題（桜蔭中2020）

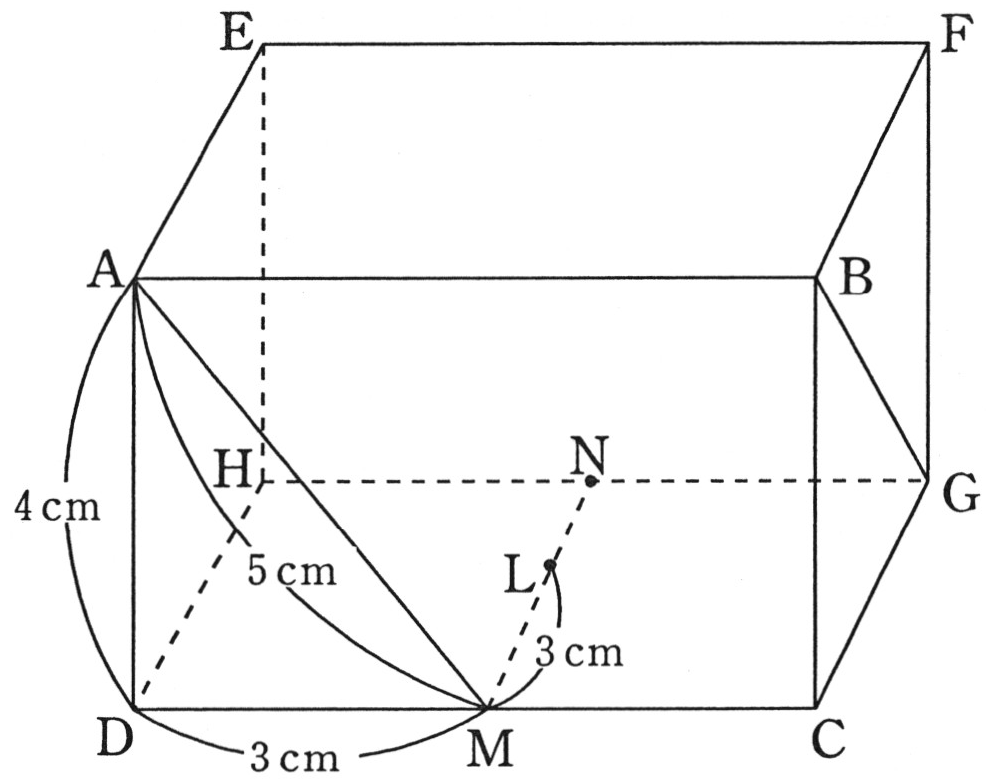
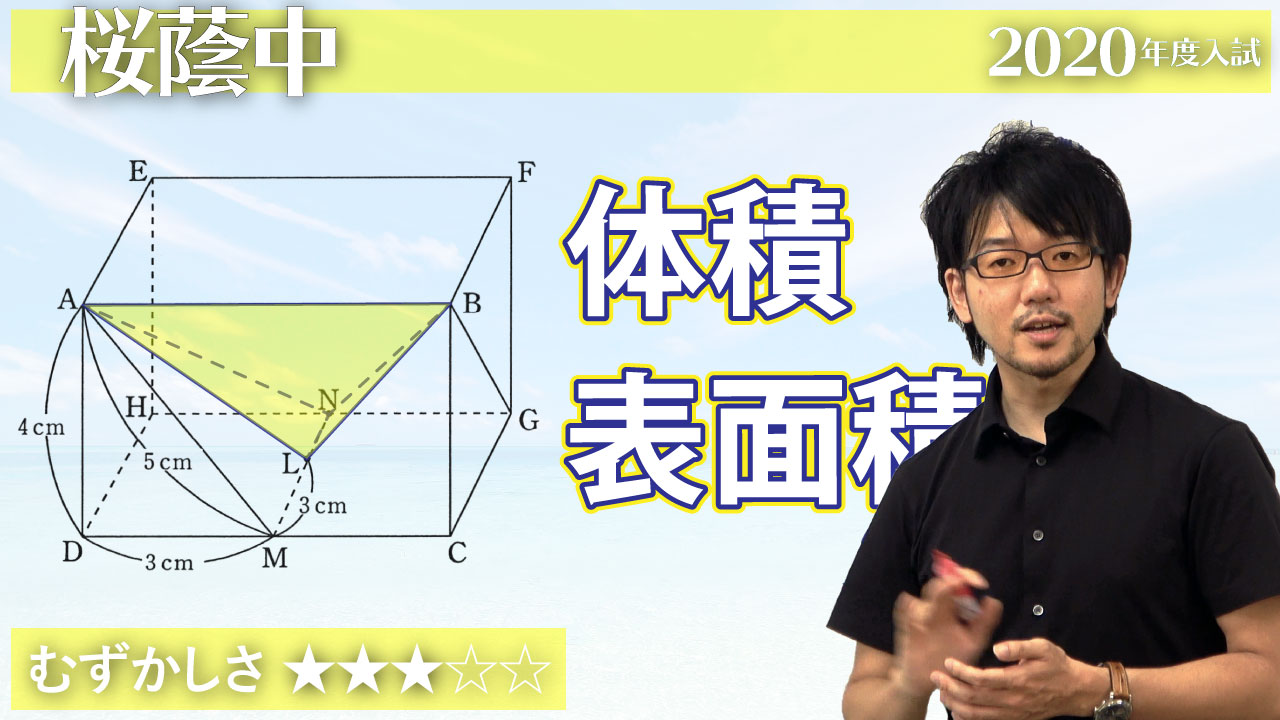
図の直方体 ABCD – EFGH において，辺 DC，HG の真ん中の点をそれぞれ M ，N とします。また MN 上に点 L があり，AD = 4 ㎝，DM = 3 ㎝，ML = 3 ㎝，AM = 5 ㎝ です。三角形 ADM を拡大すると，三角形 GCB にぴったり重なります。三角形 GCB の一番短い辺は BC です。このとき次の問いに答えなさい。

( 1 ) 次の（　）にあてはまる数を答えなさい。
辺 GC の長さは（ア）㎝，BG の長さは（イ）㎝ です。

( 2 )三角形 ANB ，三角形 ALB ，三角形 ALN ，三角形 BLN で囲まれた立体 ALBN の体積を求めなさい。

( 3 ) ① 三角形 ANB の面積を求めなさい。
　 ② 立体 ALBN の表面積を求めなさい。