算数の問題（広尾学園中2020）

太郎君と花子さんは次の問題について考えています。

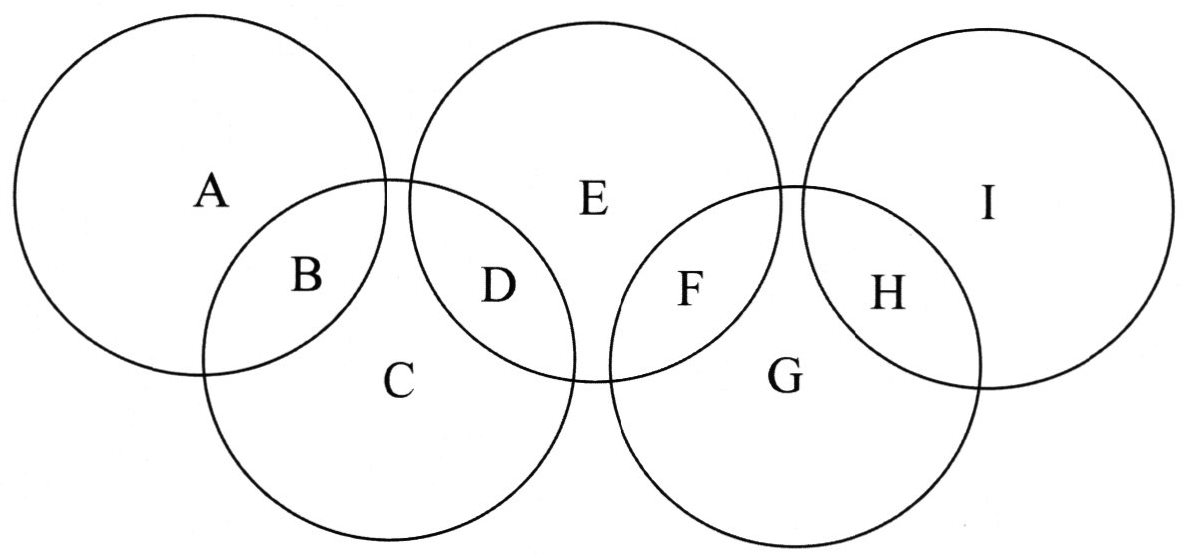
問題
次の図のように，５つの円が少しずつ重なった図があります。この図を，円か重なっている４つの部分Ｂ，Ｄ，Ｆ，Ｈと，円が重なっていない５つの部分Ａ，Ｃ，Ｅ，Ｇ，Ｉに分けます。ＡからＩに１から９の異なる整数を１つずつ入れなさい。ただし，それぞれの円に囲まれている整数の和がすべて等しくなるようにしなさい。この問題に対する太郎君と花子さんの以下の対話を参考にして，次の問いに答えなさい。

太郎：１から９までの整数をすべて足すと 45 になるし，円は５つあるから，１つの円に囲まれる 整数の和は 455 で９にすればいいのかな？
花子：それはおかしいわね。だって，９が含まれる円は，囲んでいる整数の和が９を超えてしまうわ。
太郎：言われてみるとそうだね。何がいけなかったのだろう。
花子：Ａが関係する円は１つだけど，Ｂが関係する円は２つあるから，それぞれの円に入る整数の和の合計を考えるときは，Ｂ，Ｄ，Ｆ，Ｈに入る数を２回足さないといけないわ。
太郎：そうか！１つの円に入る整数の和を ◯ とすると
　　　５× ◯ -（ Ａ – Ｂ + Ｃ + Ｄ + Ｅ + Ｆ + Ｇ + Ｈ + I ）+ Ｂ + Ｄ + Ｆ + Ｈが成り立つね。
花子：そうね。そうするとＢ + Ｄ + Ｆ + Ｈは ▢ の倍数になるわね。
太郎：そうだね。それを基準にうまく考えられそうだね。

（ 1 ）▢ に入る１以外の整数を答えなさい。
（ 2 ）１つの円に入る整数の和は，最も大きくなる場合でいくつになるか答えなさい。求める過程もかきなさい。