算数の問題（本郷中2020）

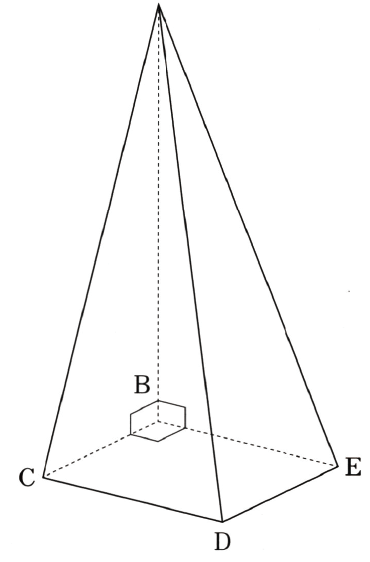
次の図のような四角すい ABCDE の内部に、次の 2 つの条件をみたす立体を作ります。

条件 1 ．三角形 ABC と三角形 BCD は作った立体の側面と底面です。
条件 2 ．作った立体を四角すいの側面 ABE に平行な平面で切ると、どこで切っても断面は直角三角形になります。辺 AB の長さは 2 ㎝ で、正方形 BCDE の 1 辺は 1 ㎝ です。
このとき、次の問いに答えなさい。

（ 1 ）条件 2 をみたす断面が直角二等辺三角形になるとき、この直角二等辺三角形の面積は何 ㎠ ですか。
（ 2 ）作った立体を辺 BC のまわりに 1 回転させてできる立体の体積は ▢ × 3.14 ㎤ になります。▢ にあてはまる分数を答えなさい。ただし、円周率は 3.14 とします。