JGの過去問
算数の問題(女子学院中2020)
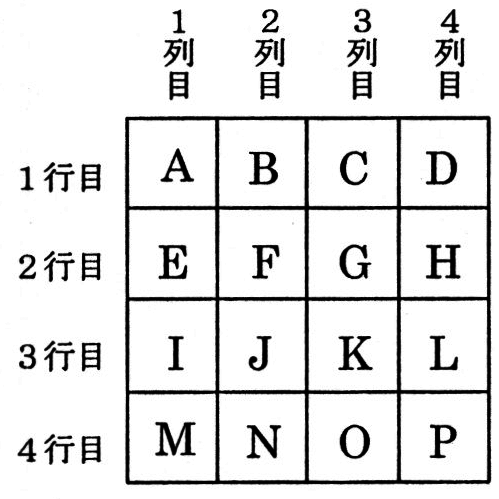
次のように,AからPまでに,ある整数が入っている表があります。この表に,次の規則に従って ○ か × の印をつけます。
① AからPまでの数の1つに ○ をつけ,その数と同じ行,同じ列に並んでいる印のついていない数すべてに × をつける。 ② 印のついていない残りの数の1つに ○ をつけ,その数と同じ行,同じ列に並んでいる印のついていない数すべてに × をつける。 ③ もう一度 ② を行い,残った数に ○ をつける。
この表では,どこを選んで ○ をつけていっても,① から ③ の作業をした後に ○ のついた数の和がいつでも同じになることが分かりました。 (1) ① から ③ の作業をした後に ○ のついた数は全部で □ 個あり,それらの数の和はいつでも □ です。 (2) Aに入っている数は □ ,Gに入っている数は □ です。 (3) この表に入っている一番大きい数は □ 一番小さい数は □ です。